So far, we’ve wrapped up Part 1 of this series, which was all about the convolution layer (Everything you need to know about CNNs Part 1: Convolution Layer). We are still hanging out in the feature extraction section and today we’ll spend all our time focusing on the unsung hero of CNNs — the Rectified Linear Unit, better known as ReLU.
ReLU is the most common activation function used in CNNs and it makes our lives easier in ways you can’t imagine. But before we jump into ReLU, let’s talk briefly about activation functions in general.
You can stack as many layers as you want and do all sorts of fancy feature extraction, but without your activation function the network won’t learn much of anything!
ACTIVATION FUNCTIONS
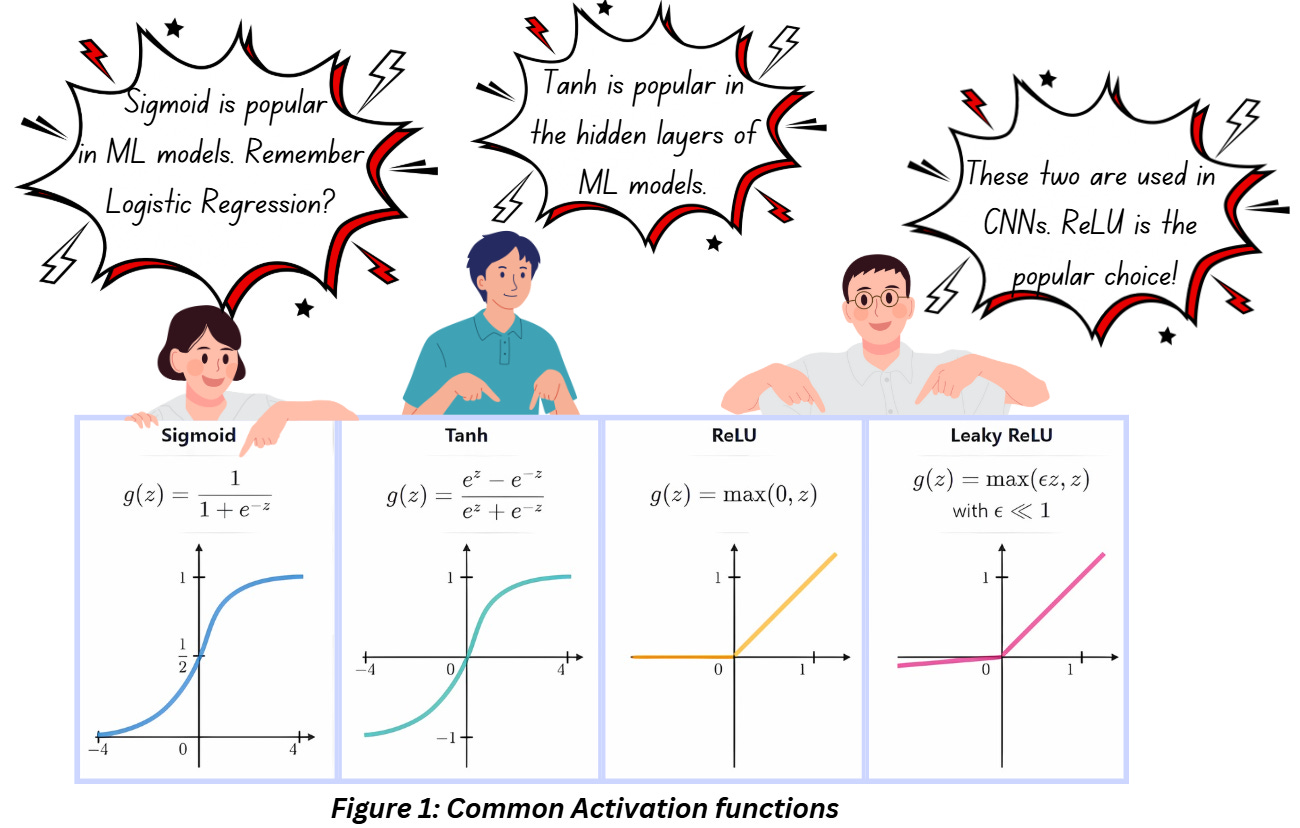
An activation function is a mathematical function that is applied to the output of a neuron to introduce non-linearity into the model. That’s all it does! Without activation functions, neural networks would just be a bunch of linear operations like matrix multiplication. The network would learn absolutely nothing about the complexities in the data. Check out the list of common activation functions,
Look at Figure 1 carefully, do you notice what’s common in all the images?
In each case, we are transforming (or mapping) the values on the x-axis to a different range. For instance, sigmoid is capping all values of x between 0 and 1, tanh is fitting the same values to -1 and 1(this symmetry makes tanh quite popular, we always love a function that can centre the values at 0). Compared to these two, ReLU and Leaky ReLU look straightforward, but we are still limiting the values where x is negative. This process of mapping these values to a different range gets rid of the linearity that we don’t want to avoid (even ReLU looks like a straight line but there’s a discontinuity at 0 which helps our case.
Why are activation functions so important?
Let’s start with the most obvious thing – post the activities of the convolution layer and the addition of the bias term (we’ll talk about this in a later part in the series), the output image may have values that are very large or very small. This is never good. If you’ve worked with ML before, you’ll be aware that we love normalized values set within a particular range because it helps stabilize the training process. Figure 1 makes it obvious that our activation functions are doing that.
The second part of the answer lies in our continued obsession with non-linearity.
Non-linearity indicates that the output cannot be calculated using a linear combination of inputs. Let’s take the example of predicting the price of a person’s house based on their salary, monthly expenditure, family size, location and a bunch of other factors. You might think if a person has a higher salary they’ll have a more expensive house. Or if someone has a family of five members, they’ll probably want a bigger house, i.e., a more expensive house. But that’s not necessarily the case. The relationship between the inputs (features in our context) and output (price of the house) will be a bit more complex!
Most real-world data is non-linear and we want our model to be able to pick up on the complexity of the data. Activation functions help our networks learn these non-linear relationships by introducing non-linear behavior using activation functions which significantly impacts the model’s performance.
I feel now’s a good time to start using a standard architecture for our reference. How about using VGG16?
VGG16 OVERVIEW
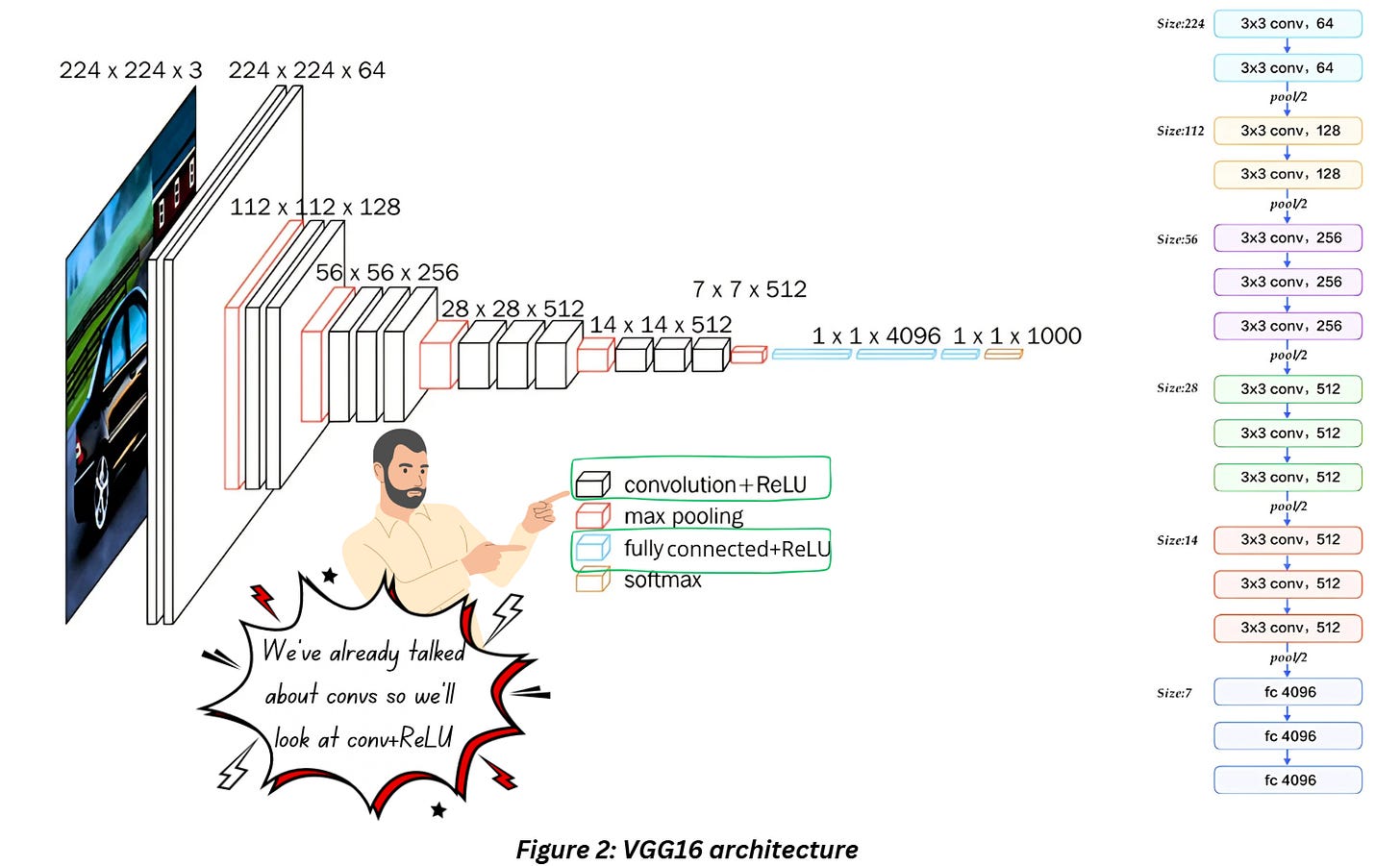
We won’t drill too deep in this blog but let’s have a look at the architecture before resuming our conversation about ReLU. VGG16 looks like this,
If you look at the legend in Figure 2 - notice that the primary components used are convolution, max pooling, fully connect layers with a softmax at the end for the classification purpose. We can use this for just feature extraction by simply getting rid of the some of the final layers. Based on what you’re training task is, you can choose to train some of the layers while freezing the others. But today we’ll just look at the activation layer.
RECTIFIED LINEAR UNIT
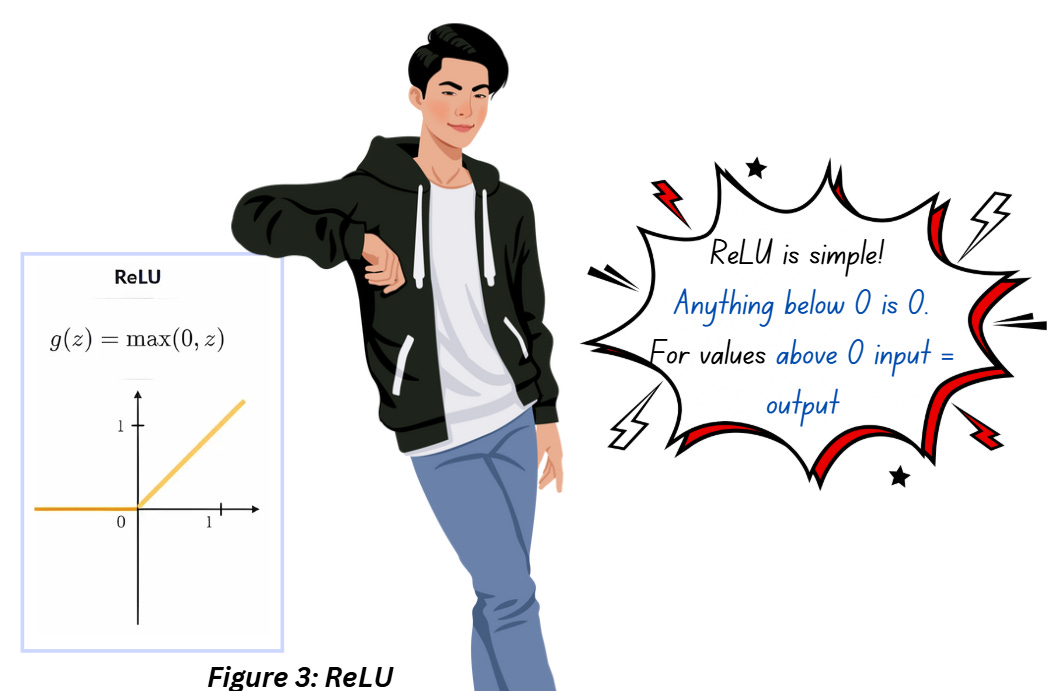
Check out the legend of the in Figure 2, you’ll notice ReLU is used along with convolution and fully connected layers. Just like any other activation function, ReLU introduces non-linearity and the way it works is shown in the graph below,
What happens to the convolution output during the activation process?
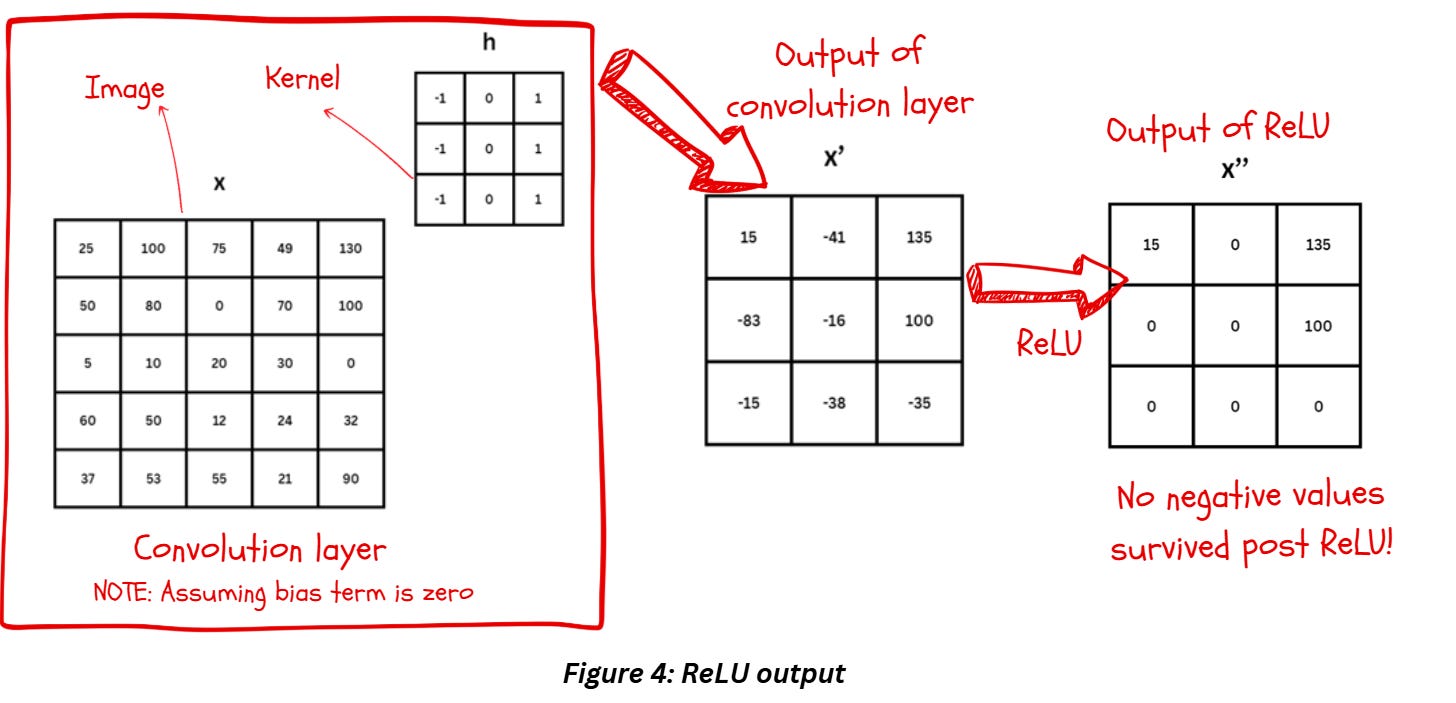
Figure 4 shows the fate of image x after convolution and ReLU when we assume the bias term is zero. Bias weights are just constants that are added to convolution layer’s output. Each convolution layer has 2 sets of weights - first there are the kernel values or kernel weights and then there are the bias weights. Bias weights are used to offset the results, when it’s set to zero, it’ll have no impact.
Notice how all the negative quantities are set to zero during ReLU while the positive values remain unchanged. Compared to Sigmoid and Tanh, ReLU feels a bit too simple, doesn’t it? But there’s a reason for it – we want this step to be simple for a reason!
What happens if we use a sigmoid function instead of ReLU in a deep CNN? ReLU is non differentiable at point zero which doesn’t always sit well with researchers. Sigmoid has been used in classification tasks before, sigmoid seems to do a pretty good job at capping the values in a range, something ReLU doesn’t seem to be doing with the positive values. To answer this, we’ll have to go through a list of things ReLU does well,
Things we love about ReLU
1) ReLU is easy to differentiate if we assume the derivative at point zero to be zero
2) The simplicity of ReLU makes it super handy in the backpropagation step where we have to calculate a tonne of partial derivatives to perform the weight updates.
3) The lack of exponential terms (which we see in the expressions of sigmoid and tanh) gets rid of two massive issues in deep networks known as the vanishing gradient problem and the exploding gradient problem
I will dedicate a separate article to the above three points, it’s pretty cool to look at the math!
Things ReLU could do better
1) Converting all the negative values to zero might not be the best idea. We do lose out information and it might hamper with the model’s ability to fit properly
2) Converting negative values to zero also results in something known as the Dying ReLU problem. In this situation there is no gradient flowing through the neuron during backpropagation, this causing the weights of these neurons to not get updated.
LEAKY RELU
Leaky ReLU is just like ReLU, with the exception of a small gradient value for negative inputs. In a way it suppresses the activity of these neurons without entirely getting rid of them.
However, this approach might require some experimentation with the hyperparameters of the model like learning rate in order to get consistent results.
PARAMETRIC RELU
This is an advanced version of ReLU and Leaky ReLU where we let the slope of the Leaky ReLU function become a learnable parameter.
Does this make the process more time consuming? Yes.
Does is improve model performance? YES.
But don’t go around using this for every case, given the computation cost, it’s best to use this for complex problem statements.
Can I modify the threshold of ReLU from 0 to something else?
Sure you can. Tensorflow allows you to modify a bunch of parameters including the threshold value. The parameters and the default values are shown below, Along with threshold, you can put a cap on the output value using the max_value parameter which will add an upper limit to the output values. Negative slope parameter is used for leaky relu to determine the slope for the negative values.
Turns out negative threshold based ReLUs are a different category known as Margin ReLU.
Are there other activations used in CNNs apart from the ReLU family?
Yeah, there are a bunch of other activation functions like Mish. But ReLU does a fairly good job in most cases.
REFERENCES
Standford Deep Learning https://stanford.edu/~shervine/teaching/cs-229/cheatsheet-deep-learning
Non-linearity: https://stats.stackexchange.com/questions/275358/why-is-increasing-the-non-linearity-of-neural-networks-desired
Universal Approximation theorem: https://en.wikipedia.org/wiki/Universal_approximation_theorem
Universal Approximation theorem and NN: https://towardsdatascience.com/can-neural-networks-really-learn-any-function-65e106617fc6
Leaky and PreLU: https://medium.com/@juanc.olamendy/understanding-relu-leakyrelu-and-prelu-a-comprehensive-guide-20f2775d3d64
Modifying ReLU thresholds in Tensorflow: https://www.tensorflow.org/api_docs/python/tf/keras/activations/relu
ReLU detailed blog: https://machinelearningmastery.com/rectified-linear-activation-function-for-deep-learning-neural-networks/